This project is a very simple application of genetic programming to the facinating "iterated prisonner's dilemma" game.
According to Wikipedia : > Albert W. Tucker formalized the game with prison sentence rewards and named it, "prisoner's dilemma" (Poundstone, 1992), presenting it as follows: Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of communicating with the other. The prosecutors lack sufficient evidence to convict the pair on the principal charge. They hope to get both sentenced to a year in prison on a lesser charge. Simultaneously, the prosecutors offer each prisoner a bargain. Each prisoner is given the opportunity either to: betray the other by testifying that the other committed the crime, or to cooperate with the other by remaining silent. The offer is: * If A and B each betray the other, each of them serves 2 years in prison * If A betrays B but B remains silent, A will be set free and B will serve 3 years in prison (and vice versa) * If A and B both remain silent, both of them will only serve 1 year in prison (on the lesser charge)I chose, to be clearer, instead of the years in prison system, a point system presented in an article from Pour la Science, written by the french searcher J.-P. DELAHAYE
| / | P1 cooperates | P1 betrays |
|---|---|---|
| P2 cooperates | P2 : 3 / P1 : 3 | P2 : 0 / P1 : 5 |
| P2 betrays | P2 : 5 / P1 : 0 | P2 : 1 / P1 : 1 |
In a 1 Vs. 1 game, the best strategy, the one that will always get you at least as many, and maybe more points than your opponent will be to betray. That is why the iterated version is very interesting.
When many people play together, everyone plays 1000 rounds agains every players, including himself, betraying is a very bad strategy, because after several round of betraying, the opponent will certainly start to also betray and you will both get a very low amount of point (1 each) instead of both cooperating and winning a higher amount of points (3 each). Therefore, other strategies are to be found.I used, for my study, the 12 strategies presented by J.-P. DELAHAYE in his article.
Using these 12 strategies, I tried creating new determinist strategies using a genetic algorithm that will try to get the best score possible.The goal is to optimise a vector of continue values between 0 and 1 that determine the next move that will be played based on coefficient calculated upon the statistics of the precedent rounds.
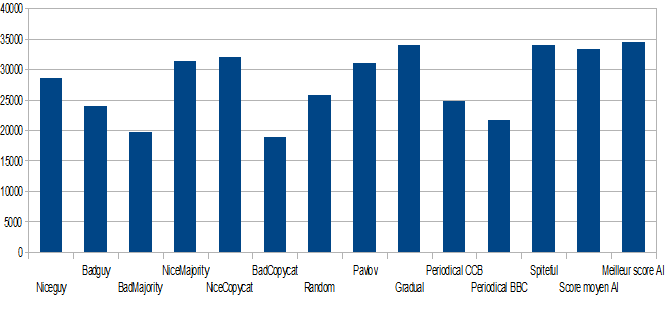
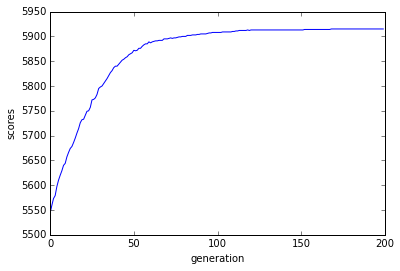
The results, although not perfect, were really promissing and open to ameliorations. Three very interesting points were to be recorded : * The average results were quite above average :  * The best score I had after many tries, comming from a surprisingly good strain got the best score of all the strategies : 
Here is the histogram of all the strategies scores (it's an average since it changes every time, considering that random changes everybody's score)
- Finally, the algorithm has a very good adaptability capacity, since it got a very good score when I tried it with only two strategies, 'always betray' and 'always cooperates", where the best score you can have is 6000 (always betray) :
